6. Mezní otáčky a vibrace
Ložiska ZKL nakupujte od autorizovaných distributorů
Najít distributora
Najít distributora
Technická podpora:
6.1 Tření v ložisku
Tření v ložisku závisí na zatížení, provozních otáčkách, mazivu, typu a velikosti ložiska. Tření má potom zásadní vliv na vývin tepla v ložisku a tedy i jeho provozní teplotu.Celkový valivý odpor v ložisku je daný součtem:
- valivého a smykového tření ve všech místech kontaktu (valivý kontakt, styk mezi valivými tělesy a klecí, resp. vodícími plochami)
- tření v mazivu
- popř. smykového tření třecího těsnění
6.1.1 Odhad třecího momentu
Třecí moment lze určit např. podle následujícího vztahu:
M = 0,5·μ·P·d
kde M [N·mm] … třecí moment ložiska
μ [ - ] … konstantní součinitel tření ložiska (viz tab. 6.1)
P [N] … ekvivalentní dynamické zatížení ložiska
d [mm] … průměr díry ložiska
Daný vztah však s dostatečnou přesností platí pouze za předpokladu dobrého mazání, normálních provozních podmínek a zatížení ložiska P = 0,1·C.
M = 0,5·μ·P·d
kde M [N·mm] … třecí moment ložiska
μ [ - ] … konstantní součinitel tření ložiska (viz tab. 6.1)
P [N] … ekvivalentní dynamické zatížení ložiska
d [mm] … průměr díry ložiska
| Typ ložiska | Součinitel tření μ |
| Kuličková ložiska | 0,0015 |
| Kuličková ložiska skosoúhlým stykem | |
| - jednořadá | 0,0020 |
| - dvouřadá | 0,0024 |
| - čtyřbodová | 0,0024 |
| Naklápěcí kuličková ložiska | 0,0010 |
| Válečková ložiska | |
| - sklecí při Fa = 0 | 0,0011 |
| - splným počtem válečků při Fa = 0 | 0,0020 |
| Kuželíková ložiska | 0,0018 |
| Soudečková ložiska | 0,0018 |
| Axiální kuličková ložiska | 0,0013 |
| Axiální válečková ložiska | 0,0050 |
| Axiální soudečková ložiska | 0,0018 |
Daný vztah však s dostatečnou přesností platí pouze za předpokladu dobrého mazání, normálních provozních podmínek a zatížení ložiska P = 0,1·C.
6.1.2 Výpočet třecího momentu
Celkový třecí moment M [N·mm] se skládá z hydrodynamického momentu tření M0 [N·mm] nezatíženého ložiska, který vzniká od brodění rotujících částí ve viskózním prostředí, a z momentu valivého tření M1 [N·mm]:
M = M0 + M1
Hydrodynamický moment tření závisí na mazání, velikosti ložiska a otáčkách:
M0 = f0·dm3·(ν·n)k0
kde f0 [ - ] … konstanta mazání pro ložiska téže řady, téhož provedení a přesnosti
dm [mm] … střední průměr ložiska
ν [m2·s-1] … kinematická viskozita maziva
n [min-1] … otáčky
k0 [ - ] … konstanta rovná 2/3
Moment valivého tření závisí na zatížení, statické únosnosti a velikosti ložiska:
M1 = fα´·F·dm·(F/C0)c
kde fα´ [ - ] … funkce směru zatížení pro ložiska téže řady, téhož provedení a přesnosti
F [N] … zatížení
dm [mm] … střední průměr ložiska
C0 [N] … základní statická únosnost ložiska
c [ - ] … experimentálně určený exponent
Přesnější výpočtový model poté počítá se čtyřmi zdroji tření:
M = Mrr + Msl + Mseal + Mdrag
kde M [N·mm] … celkový třecí moment
Mrr [N·mm] … moment valivého tření
Msl [N·mm] … moment smykového tření
Mseal [N·mm] … třecí moment v ložisku
Mdrag [N·mm] … třecí moment způsobený broděním
Výpočet pomocí tohoto modelu je však již značně komplikovaný.
M = M0 + M1
Hydrodynamický moment tření závisí na mazání, velikosti ložiska a otáčkách:
M0 = f0·dm3·(ν·n)k0
kde f0 [ - ] … konstanta mazání pro ložiska téže řady, téhož provedení a přesnosti
dm [mm] … střední průměr ložiska
ν [m2·s-1] … kinematická viskozita maziva
n [min-1] … otáčky
k0 [ - ] … konstanta rovná 2/3
Moment valivého tření závisí na zatížení, statické únosnosti a velikosti ložiska:
M1 = fα´·F·dm·(F/C0)c
kde fα´ [ - ] … funkce směru zatížení pro ložiska téže řady, téhož provedení a přesnosti
F [N] … zatížení
dm [mm] … střední průměr ložiska
C0 [N] … základní statická únosnost ložiska
c [ - ] … experimentálně určený exponent
Přesnější výpočtový model poté počítá se čtyřmi zdroji tření:
M = Mrr + Msl + Mseal + Mdrag
kde M [N·mm] … celkový třecí moment
Mrr [N·mm] … moment valivého tření
Msl [N·mm] … moment smykového tření
Mseal [N·mm] … třecí moment v ložisku
Mdrag [N·mm] … třecí moment způsobený broděním
Výpočet pomocí tohoto modelu je však již značně komplikovaný.
6.2 Mezní otáčky
Provozní otáčky ložisek jsou limitovány vnitřní konstrukcí ložiska, jeho přesností a velikostí, vůlí v ložisku, způsobem mazání a konstrukcí uložení, které má vliv na odvádění vznikajícího tepla z ložiska. Proto je nutné všem uvedeným vlivům při navrhování vhodného ložiska věnovat pozornost.Mezními otáčkami rozumíme takové otáčky, při nichž je za daných provozních podmínek dosaženo tepelné rovnováhy mezi teplem vznikajícím v ložisku a teplem, které je z ložiska odváděno.
Na základě experimentálních zkoušek a praktických aplikací lze konstatovat, že existují maximální otáčky, které by neměly být překročeny z technických důvodů nebo z důvodu velmi vysokých nákladů, které by si vyžádalo udržení provozní teploty na přijatelné úrovni.
Pokud by ložisko mělo pracovat s vyššími otáčkami, než jsou mezní, je nutné změnit mazání a odvod tepla, popř. konstrukci klece, resp. celého ložiska. Pro vyšší otáčky se například doporučují ložiska ve vyšší přesnosti s masivní klecí vedenou na některém z ložiskových kroužků a mazání oběhem oleje nebo olejovou mlhou.
6.2.1 Definice mezních otáček ZKL
V tabulkové části katalogu jsou uváděny mezní otáčky, které jsou stanoveny jako tepelné referenční otáčky v souladu s ISO 15312:2003. Referenční podmínky, které definují tepelnou rovnováhu, jsou: zvýšení teploty o 50°C nad okolní teplotu a zatížení ve výši 5% statické únosnosti ložiska. Tyto podmínky platí pro nezakrytá ložiska s normální radiální vůlí.
Mezní otáčky valivého ložiska, které jsou uvedeny v tabulkové části katalogu, jsou referenční otáčky pro mazání olejem bez EP přísad s kinematickou viskozitou při teplotě 70°C: 12 mm2/s, resp. 24 mm2/s pro axiální ložiska s čárovým stykem.
Mezní otáčky pro mazání plastickým mazivem jsou přibližně o 20% nižší.
Výpočet mezních otáček vychází z následující podmínky tepelné rovnováhy:
n_mez=(W_s (T_(D,max)-T_o )-∑▒Q_i )/jM
kde Ws [W·K-1] … součinitel chlazení
TD,max [K] … max. teplota na vnějším kroužku
To [K] … teplota okolí
Q [J] … množství tepla
j [ - ] … mechanický ekvivalent
M [N·mm] … celkový třecí moment
Po úpravě a dosazení dostaneme rovnici pro mezní otáčky:
n^(5/3)+n (f_α^´∙F∙(F/C_0 )^c)/(f_0^´∙d_m^2∙ν^(2/3) )-(W_s (T_(D,max)-T_o )-∑▒Q_i )/(j∙f_0^´∙d_m^3∙ν^(2/3) ) = 0
kde f0´ [ - ] … funkce vlivu mazání pro ložiska téže řady, téhož provedení a přesnosti
Daná rovnice má pouze jeden reálný kořen, přičemž tento kořen fyzikálně odpovídá hodnotě mezních otáček.
Přibližně lze hodnotu mezních otáček stanovit podle následujících vztahů:
pro radiální ložiska: n_mez=(A∙f)/d_m
kde A [ - ] … koeficient závislý na ložiskové řadě a mazání
f [ - ] … funkce vlivu velikosti a zatížení ložiska
pro axiální ložiska: n_mez=(A∙f)/√(D∙H)
kde D [mm] … vnější průměr ložiska
H [mm] … výška ložiska
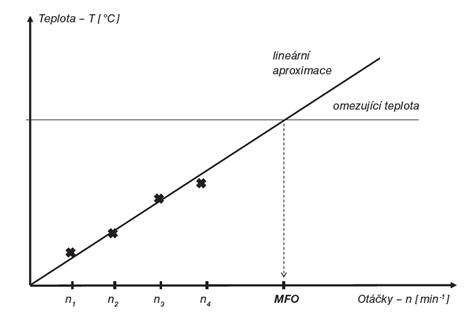
Obr. 6.1
Součinitel A pro stanovení přibližných mezních otáček je uveden v tabulce 6.2
Mezní otáčky valivého ložiska, které jsou uvedeny v tabulkové části katalogu, jsou referenční otáčky pro mazání olejem bez EP přísad s kinematickou viskozitou při teplotě 70°C: 12 mm2/s, resp. 24 mm2/s pro axiální ložiska s čárovým stykem.
Mezní otáčky pro mazání plastickým mazivem jsou přibližně o 20% nižší.
Výpočet mezních otáček vychází z následující podmínky tepelné rovnováhy:
n_mez=(W_s (T_(D,max)-T_o )-∑▒Q_i )/jM
kde Ws [W·K-1] … součinitel chlazení
TD,max [K] … max. teplota na vnějším kroužku
To [K] … teplota okolí
Q [J] … množství tepla
j [ - ] … mechanický ekvivalent
M [N·mm] … celkový třecí moment
Po úpravě a dosazení dostaneme rovnici pro mezní otáčky:
n^(5/3)+n (f_α^´∙F∙(F/C_0 )^c)/(f_0^´∙d_m^2∙ν^(2/3) )-(W_s (T_(D,max)-T_o )-∑▒Q_i )/(j∙f_0^´∙d_m^3∙ν^(2/3) ) = 0
kde f0´ [ - ] … funkce vlivu mazání pro ložiska téže řady, téhož provedení a přesnosti
Daná rovnice má pouze jeden reálný kořen, přičemž tento kořen fyzikálně odpovídá hodnotě mezních otáček.
Přibližně lze hodnotu mezních otáček stanovit podle následujících vztahů:
pro radiální ložiska: n_mez=(A∙f)/d_m
kde A [ - ] … koeficient závislý na ložiskové řadě a mazání
f [ - ] … funkce vlivu velikosti a zatížení ložiska
pro axiální ložiska: n_mez=(A∙f)/√(D∙H)
kde D [mm] … vnější průměr ložiska
H [mm] … výška ložiska
Experimentálně se poté mezní frekvence otáčení stanovuje při radiálním zatížení, které odpovídá trvanlivosti Lh = 104 ÷ 105 hodin tak, že se stupňovitě mění otáčky a zaznamenává se ustálená teplota na vnějším kroužku ložiska. Mezní otáčky jsou poté určeny jako průsečík lineární aproximace naměřených hodnot a omezující referenční teploty (obr. 6.1).

Obr. 6.1
Součinitel A pro stanovení přibližných mezních otáček je uveden v tabulce 6.2
| Typ ložiska | Součinitel A |
| Jednořadá kuličková | 500 000 |
| Jednořadá kuličková s těsněním RS a 2RS | 300 000 |
| Jednořadá kuličková s kosoúhlým stykem | |
| α≤15° | 500 000 |
| α=26° | 420 000 |
| α=40° | 400 000 |
| Dvouřadá kuličková s kosoúhlým stykem | 320 000 |
| Jednořadá válečková | 500 000 |
| Dvouřadá válečková | 500 000 |
| Dvouřadá soudečková, kromě řady 232 | 250 000 |
| Dvouřadá soudečková řady 232 | 200 000 |
| Kuželíková, kromě řady 313 | 250 000 |
| Kuželíková řady 313 | 200 000 |
| Axiální kuličková | 100 000 |
| Axiální válečková | 100 000 |
| Axiální soudečková | 200 000 |
6.2.2 Zvláštní případy provozních otáček
V případě velmi nízkých otáček nedochází k vytvoření elastohydrodynamického mazivového filmu v místě valivého kontaktu. V takovýchto uloženích je poté nutné používat maziva s obsahem EP přísad.
Dalším zvláštním případem jsou oscilační pohyby. U tohoto typu pohybu dochází ke změně smyslu otáčení dříve, než ložisko dokončí jednu otáčku. V okamžiku, kdy dochází k změně smyslu otáčení, jsou otáčky nulové a hydrodynamický mazivový film tak není zachován. V daném případě dochází k vytvoření mazivového filmu v oblasti smíšeného mazání. Pro oscilační pohyby není možné stanovit mezní otáčky, protože horní mez není určena tepelnou rovnováhou, nesetrvačnými silami. Během každé změny smyslu pohybu dochází k nebezpečí, že setrvačnost způsobí krátkodobé prokluzování valivých těles a poškození oběžných drah. Přípustné zrychlení, resp. zpomalení, je závislé na hmotnosti valivých elementů a klece, mazání a zatížení ložiska.
Dalším zvláštním případem jsou oscilační pohyby. U tohoto typu pohybu dochází ke změně smyslu otáčení dříve, než ložisko dokončí jednu otáčku. V okamžiku, kdy dochází k změně smyslu otáčení, jsou otáčky nulové a hydrodynamický mazivový film tak není zachován. V daném případě dochází k vytvoření mazivového filmu v oblasti smíšeného mazání. Pro oscilační pohyby není možné stanovit mezní otáčky, protože horní mez není určena tepelnou rovnováhou, nesetrvačnými silami. Během každé změny smyslu pohybu dochází k nebezpečí, že setrvačnost způsobí krátkodobé prokluzování valivých těles a poškození oběžných drah. Přípustné zrychlení, resp. zpomalení, je závislé na hmotnosti valivých elementů a klece, mazání a zatížení ložiska.
6.3 Vznik vibrací v ložisku
Vnímání vibrací zpravidla souvisí se šířením hluku. Ložisko ale většinou není zdrojem hluku. Hluk je pouze slyšitelným efektem vibrací, které jsou způsobeny přímo či nepřímo ložiskem, na souvisejících dílech. To je důvod toho, proč jsou většinou problémy s hlukem spojovány s otázkou vibrací samotného ložiska nebo celého uložení.U radiálně zatíženého ložiska dochází při provozu ke změně počtu valivých elementů, které přenášejí zatížení. Vlivem tohoto efektu dochází k posouvání ve směru působení zatížení. Výsledným vibracím sice nelze zabránit, ale lze je redukovat působením axiálního předpětí, které zajistí zatížení všech valivých elementů.
V případě místního poškození oběžných drah, resp. valivých elementů, které může vzniknout při nesprávné manipulaci nebo chybné montáži, dochází k převalování poškozených částí ložiska, což vyvolává vibrace. Zdroj vibrací (poškozený díl) lze určit pomocí frekvenční analýzy vibrací.
U ložisek pracujících v znečištěném prostředí může dojít k proniknutí nečistot do ložiska, v němž se přes tyto nečistoty převalují valivé elementy. Velikost vyvolaných vibrací závisí na množství, velikosti a struktuře nečistot. Nedochází k vzniku typických frekvencí, může se však ozývat slyšitelný hluk.
6.3.1 Frekvenční charakteristiky ložisek
Frekvence impulsů vibrací vzniklé převalováním poškozených částí ložiska má jednoduchý vztah k vnitřní geometrii ložiska a k frekvenci otáčení hřídele. Tyto vztahy se dají popsat rovnicemi, které definují frekvence závad na jednotlivých součástech ložiska. Uvedené rovnice jsou idealizovány, protože nepředpokládají prokluzy valivých těles. V rovnici pro vadu na kuličce se předpokládá, že se vada za jednu otáčku valivého tělesa dotkne vnitřního i vnějšího kroužku.
Frekvence při závadě na vnějším kroužku (BPFO)
BPFO = z/2 . n . (1 - Dw/dm . cos α)
Frekvence při závadě na vnitřním kroužku (BPFI)
BPFI = z/2 . n . (1 + Dw/dm . cos α)
Frekvence při závadě na kuličce či válečku (BSF)
BSF = dm /2Dw . n . (1 - (Dw/dm. cosα)2)
Frekvence při závadě na kleci (FTF)
FTF = n/2 . (1 - Dw/dm . cos α)
Kde:
Dw ... průměr valivého tělesa (mm)
dm ... roztečný průměr ložiska (mm)
z ... počet valivých těles
n ... frekvence otáčení hřídele (s-1)
α ... stykový úhel
Frekvenční analýzy vibrací umožňují zjistit, který díl ložiska je poškozený. Při výpočtu frekvenčních charakteristik doporučujeme spolupracovat s technicko-konzultačními službami ZKL.
Frekvence při závadě na vnějším kroužku (BPFO)
BPFO = z/2 . n . (1 - Dw/dm . cos α)
Frekvence při závadě na vnitřním kroužku (BPFI)
BPFI = z/2 . n . (1 + Dw/dm . cos α)
Frekvence při závadě na kuličce či válečku (BSF)
BSF = dm /2Dw . n . (1 - (Dw/dm. cosα)2)
Frekvence při závadě na kleci (FTF)
FTF = n/2 . (1 - Dw/dm . cos α)
Kde:
Dw ... průměr valivého tělesa (mm)
dm ... roztečný průměr ložiska (mm)
z ... počet valivých těles
n ... frekvence otáčení hřídele (s-1)
α ... stykový úhel
Frekvenční analýzy vibrací umožňují zjistit, který díl ložiska je poškozený. Při výpočtu frekvenčních charakteristik doporučujeme spolupracovat s technicko-konzultačními službami ZKL.
6.3.2 Vliv ložiska na vibrace uložení
Tuhost ložiska je v mnoha uloženích řádově stejná jako tuhost souvisejících dílů. Volbou správného ložiska, uspořádáním ložisek v uložení, vhodným předpětím nebo vůlí lze tedy snížit vibrace uložení. Pokud není možné řešení vibrací pomocí volby ložiska a jeho uspořádání v uložení, lze vibrace snížit i dalšími úpravami uložení, například vložením pružného členu, který bude vibrace tlumit, nebo případnou konstrukční úpravou vedoucí k odstranění budiče kritických vibrací.
